AP Statistics: Probability jh Flashcards
Terms : Hide Images [1]
| 13688395965 | Chance experiment | Any process that generates observations whose outcomes cannot be predicted with certainty |  | 0 |
| 13688395966 | Sample space | Set of all possible outcomes of a chance experiment |  | 1 |
| 13688395967 | Event | An outcome or set of outcomes of a chance experiment |  | 2 |
| 13688395968 | Simple event | An event that consists of exactly one outcome |  | 3 |
| 13688395969 | Complement | An event that contains the set or outcomes not included by a second event; probability(event) + probability(complement) = 1 |  | 4 |
| 13688395970 | Intersection | The set of all elements that are common to 2 or more sets. | 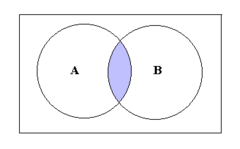 | 5 |
| 13688395971 | Union | Set of all elements that are contained in 2 or more sets |  | 6 |
| 13688395972 | Venn Diagram | A diagram that uses circles to display elements of different sets; overlapping circles show common elements |  | 7 |
| 13688395973 | Disjoint | Two non-overlapping sets; aka mutually exclusive events |  | 8 |
| 13688395974 | Mutually exclusive | Events that cannot happen at the same time |  | 9 |
| 13688395975 | Probability of an event | Number of favorable outcomes divided by the total number of possible outcomes | 10 | |
| 13688395976 | Law of large numbers | As the number of repetitions of a probability experiment increases, the empirical probability (the proportion with which a certain outcome is observed) gets closer to the theoretical probability of the outcome |  | 11 |
| 13688395977 | General Addition Rule | For any two events, A and B, the probability of A or B is the probability of A + probability of B - the joint probability of A and B | 12 | |
| 13688395978 | General Multiplication Rule | For any two events, A and B, the probability of A and B is the probability of A times the probability of B occurring given that A has occurred | 13 | |
| 13688395979 | Independent Events | Two or more events for which the outcome of one event does not affect the probability of the other; P(A) = P(A | B) |  | 14 |
| 13688395980 | Dependent Events | Two or more events in which the occurrence of one event affects the probability of the other events; do not always possess a cause-and-effect relationship |  | 15 |
| 13688395981 | Sampling without replacement | Removes each selected element from the population before the next selection is made to guarantee no element appears more than once in a single sample; probability of selecting any outcome changes after each selection |  | 16 |
| 13688395982 | Sampling with replacement | Once an element has been included in the sample, it is returned to the population and may be selected again; probability of selecting any outcome remains constant |  | 17 |
| 13688395983 | 10% sampling condition | When sampling without replacement, the change in the probability of an outcome can be regarded as insignificant and thus ignored when sampling less than 10% of a population |  | 18 |
| 13688395984 | Conditional Probability | Probability of an event occurring given that another event is known to have occurred; denoted as P(A | B) |  | 19 |
| 13688395985 | Bayes' Rule | Describes the probability of an event, based on prior knowledge of conditions that might be related to the event; for example, the prevalence of a disease in a population should be used when interpreting the results of an initial screening test | 20 | |
| 13688395986 | Empirical probability | Probability that is based on simulation, experimentation or testing; the relative frequency of a successful outcome among those trials |  | 21 |
| 13688395987 | Simulation | Modeling a problem situation or event that would be too difficult or impractical to actually perform; often used to calculate empirical probabilities |  | 22 |
| 13688395988 | Table of Random Digits | Long string of digits (0 to 9) where the digits are independent of each other (knowing one digit does not give any knowledge to predicting another digit) and where any digit (0 to 9) has an equal chance of occurring as the next digit; used for probability simulations, random selection and random assignment | 23 |
