Terms : Hide Images
| 3044079567 | Area | Area is the number of square units enclosed by the two dimensional shape. |  | 0 |
| 3044100985 | Perimeter | Perimeter is the distance around the outside of a 2D shape. |  | 1 |
| 3044102899 | Area vs perimeter | Area is the number of square units enclosed by the 2D shape. Perimeter is the distance around the outside of a 2D shape. |  | 2 |
| 3040869777 | Trapezoid | Two dimensional shape with four sides and one pair of parallel and congruent sides. |  | 3 |
| 3040920117 | Irregular Shape | Irregular shapes have sides and angles of any length and size. |  | 4 |
| 3040798124 | Circle (Radius, Diameter, Circumference) | Radius is the distance from the center to the edge. Diameter starts at one side of the circle, goes through the center and ends on the other side. Circumference is the distance around the edge of the circle. |  | 5 |
| 3040885533 | Concentric circles | Circles that have their centers at the same point. |  | 6 |
| 3032344071 | Three Dimensional Shapes or Solids | Three-Dimensional shapes can be made up of flat of curved or flat surfaces |  | 7 |
| 3032378128 | Polyhedron | A polyhedron is a three-dimensional solid figure in which each side is a flat surface. These flat surfaces are polygons and are joined at their edges. The word polyhedron is derived from the Greek poly (meaning many) and the Indo-European hedron (meaning seat or face). |  | 8 |
| 3032374351 | Face, Vertex, Edge | Each flat surface is called a FACE. EDGE is a line segment that is the intersection of two faces. VERTEX is the point that is the intersection of three or more faces. |  | 9 |
| 3044459840 | Right Rectangular Prism | A solid (3-dimensional) object which has six faces that are rectangles. The two bases are parallel and congruent. It has the same cross-section along a length, which makes it a prism. |  | 10 |
| 3040914629 | Net | A net is a two dimensional figure that can be folded to make a three dimensional object. |  | 11 |
| 3044360920 | Lateral Surface Area of a Rectangular Prism | Lateral surface area (LA) is the sum of the side faces. |  | 12 |
| 3040910371 | Total Surface Area of Rectangular Prism | Total SA = LA + Areas of 2 Bases A right prism has a set of flat surfaces called the FACES. Total Surface Area (SA) is the sum of all faces. The two bases (top and bottom faces) are parallel and congruent. |  | 13 |
| 3040906391 | Volume of Rectangular Prism | Volume is the number of cubic units to exactly fill a prism. |  | 14 |
| 3032385896 | Right Circular Cylinder | A cylinder is a closed solid that has two parallel circular bases connected by a curved surface. |  | 15 |
| 3032428745 | Surface Area Cylinder | Total SA = LA + Area of 2 Bases |  | 16 |
| 3040721540 | Volume cylinder | Volume is the number of cubic units to exactly fill a Cylinder. |  | 17 |
| 3046802753 | Pythagorean Theorem | In mathematics, the Pythagorean theorem is a relation among the three sides of a right triangle. It states that the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides. |  | 18 |
| 3046898951 | Pythagorean Triples | A Pythagorean triple consists of three positive integers a, b, and c, such that a2 + b2 = c2. Such a triple is commonly written (a, b, c), and a well-known example is (3, 4, 5). If (a, b, c) is a Pythagorean triple, then so is (ka, kb, kc) for any positive integer k. |  | 19 |
| 3046821481 | Special Right Triangles | Special Right Triangle are right triangles 1. Special Right Triangle 45º- 45º- 90º 2. Special Right Triangle 30º- 60º- 90º |  | 20 |
| 3032440992 | Right Circular Cone | A cone is a solid that has a circular base and a a single vertex. If the vertex is over the center of the base, it is called a right cone. If it is not, it is called an oblique cone. |  | 21 |
| 3040703227 | Slant Height of a Cone | The slant height is the distance from the vertex of the cone, down the side, to a point on the circumference of the base. |  | 22 |
| 3044542913 | Volume of a Cone | The volume of a cone is 1/3 the volume of a cylinder that has the same height and the same base. |  | 23 |
| 3055153648 | Volume Comparison: Cylinder and Cone | The volume of a cone is 1/3 the volume of a cylinder that has the same height and the same base. |  | 24 |
| 3032458208 | Right Square Pyramid | A three dimensional shape that has a square base and four congruent faces that meet at a point above the base called the vertex. The vertical height (h) is the perpendicular distance from the top down to the base. The 4 lateral faces are congruent isosceles triangles. The slant height (l) is the height of the lateral faces. s is the side of the base (square). |  | 25 |
| 3040699460 | Slant height of a pyramid | The slant height is used to find the total surface area of a pyramid. The slant height is not the height of the pyramid. |  | 26 |
| 3040830841 | Sphere | Surface Area: The number of square units that will exactly cover the surface of a sphere. Volume: The number of cubic units that will exactly fill a sphere. |  | 27 |
| 3040853951 | Hemisphere | Half a Sphere |  | 28 |
| 3074590099 | Using the MCAS Reference Sheet |  | 29 | |
| 3112056033 | Volume of Composite 3D shapes | First calculate the volume of each of individual figures and then find the volume of the entire composite figure. |  | 30 |
| 3113857389 | Composite figure | A figure (or shape) that can be divided into more than one of the basic figures is said to be a composite figure (or shape). |  | 31 |
| 3184939260 | Angle | An Angle is a figure formed by two rays (called SIDES or LEGS) with a common endpoint called the VERTEX (plural VERTICES). |  | 32 |
| 3184941746 | Naming Angles | Name an angle in four different ways:
 33 | | |
| 3225348666 | Classify Triangles | By Angles: Acute, Obtuse, Right, Equiangular By Sides: Equilateral, Isosceles, Scalene |  | 34 |
| 3225359290 | Classify Angles | Acute Obtuse Right Straight Reflex |  | 35 |
| 3225364164 | Supplementary Angle Pairs | A pair of angles whose sum is 180 degrees |  | 36 |
| 3225396354 | Complementary Angle Pairs | A pair of angles whose sum is 90 degrees |  | 37 |
| 3225402117 | Vertical Angle Pair | Vertical angle pairs are congruent. They are formed by two intersecting lines. |  | 38 |
| 3225405129 | Transversal line | A line that cuts across parallel lines at two distinct points. |  | 39 |
| 3225441166 | Corresponding Angle Pairs | Corresponding angle pairs are congruent |  | 40 |
| 3225445476 | Same Side Interior Angle Pairs | Same Side Interior angle pairs are supplementary (add up to 180 degrees). |  | 41 |
| 3225448539 | Alternate Interior Angle Pairs | Same Side Exterior Angle Pairs are supplementary (add up to 180 degrees). |  | 42 |
| 3225464056 | Alternate Exterior Angle Pairs | Alternate Exterior Angle pairs are congruent. |  | 43 |
| 3225483433 | Triangle Angle Sum Theorem | The sum of the three angle measures of any triangle is always180 degrees.. | 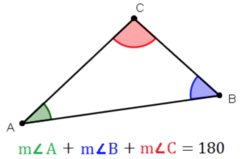 | 44 |
| 3225496323 | Triangle Exterior Angle Theorem | The measure of an exterior angle is equal to the sum of the two remote interior angles. |  | 45 |
| 3225498420 | Triangle angles | Interior and exterior angles |  | 46 |
| 3225500945 | Perpendicular Lines | Two line that intersect at 90 degree angles. |  | 47 |
| 3225509010 | Parallel Lines | Parallel lines do not intersect. They have no common point. |  | 48 |
| 3225513208 | Intersecting Lines | Intersecting lines intersect at one point. |  | 49 |
| 3225517003 | Angle Bisector | Angle bisector divides an angle into two congruent angles. |  | 50 |
| 3225520891 | Midpoint of a Line Segment | The midpoint is equidistant from the endpoints. |  | 51 |
| 3350947132 | Polygon | A 2 dimensional figure which is formed by a number of line segments, each connected end to end to form a closed shape. |  | 52 |
| 3351002455 | Regular Polygon | A polygon with all angles Congruent and all sides congruent. |  | 53 |
| 3351004650 | Irregular Polygon | A polygon with sides that are not all congruent or angles that are not all congruent |  | 54 |
| 3351008981 | Polygon Angle Sum Theorem | Number of triangles * 180 OR (n-2)*180, n = number of sides |  | 55 |
| 3351010594 | Sum of Exterior Angles of a Polygon | Always equals 360 degrees |  | 56 |
| 3351108286 | Interior Angle | An angle inside a polygon |  | 57 |
| 3351124218 | Exterior Angle | An angle formed by one side of a polygon and the extension of an adjacent side |  | 58 |
| 3351179578 | Special Quadrilateral | A four-sided polygon. |  | 59 |
| 3351197894 | Special quadrilaterals Chart | Categorize special quadrilaterals according to their properties. |  | 60 |
| 3351223952 | Consecutive or Adjacent Angles | Angles of a polygon that share a common side. |  | 61 |
| 3351236033 | Consecutive Sides | Two sides of a polygon with a common vertex. |  | 62 |
| 3351253157 | Opposite Angles | Angels that do not share a side. |  | 63 |
| 3351273271 | Parallelogram | Both pairs of opposite sides are parallel and congruent Opposite angles are congruent Consecutive angles are supplementary The diagonals bisect each other |  | 64 |
| 3351284864 | Rhombus | A parallelogram with all congruent sides The diagonals bisect opposite angles The diagonals are perpendicular bisectors |  | 65 |
| 3351304701 | Rectangle | A parallelogram with four right angles The diagonals are congruent and bisect each other |  | 66 |
| 3351391612 | Square | A parallelogram with four congruent sides and four congruent angles The diagonals are congruent The diagonals are perpendicular bisectors |  | 67 |
| 3351396846 | Trapezoid | A quadrilateral with exactly one pair of parallel sides. |  | 68 |
| 3351413795 | Isosceles Trapezoid | A trapezoid with congruent legs |  | 69 |
| 3351421324 | Kite | No parallel sides Two pairs of adjacent sides are congruent Exactly one pair of opposite angles are congruent The diagonals meet at a right angle |  | 70 |
| 3351449446 | Slope | The steepness of a line on a graph Rise over Run |  | 71 |
| 3351462268 | Slope is Zero | Slope of a Horizontal Line Equation of a horizontal line y=constant Examples: y=3, y=-4 |  | 72 |
| 3351482256 | Slope is Positive | Slope rises from left to right |  | 73 |
| 3351494886 | Slope is Negative | Slope drops from left to right |  | 74 |
| 3599284127 | Slope is Undefined | Slope of a Vertical Line. Equation of a vertical line x=constant Examples: x=3, x=-4 |  | 75 |
| 3351573600 | Line Segment | Distance between two endpoints |  | 76 |
| 3351611204 | Coordinates of a point | Point (-3, 2) |  | 77 |
| 3351645870 | Distance between two Points in the Coordinate Plane | Distance formula |  | 78 |
| 3351655718 | Distance between two Points in the Coordinate Plane using the Pythagorean Theorem | Use the Pythagorean Theorem on the coordinate plane. |  | 79 |
| 3380616541 | Midpoint Definition | The point halfway between the endpoints of a line segment is called the midpoint. A midpoint divides a line segment into two equal segments. By definition, a midpoint of a line segment is the point on that line segment that divides the segment two congruent segments. |  | 80 |
| 3380647607 | Midpoint Formula | The coordinates of the midpoint of a line segment are the average of the coordinates of its endpoints. |  | 81 |
| 3524490534 | Congruent Polygons | Corresponding angles (matching) are congruent . Corresponding sides are congruent. |  | 82 |
| 3524876887 | Ratio | A ratio is a comparison of two numbers. It is expressed as a fraction, with the numerator equal to the first quantity and the denominator equal to the second. |  | 83 |
| 3524879892 | Comparing Ratios (Fractions) | The ratios are equal if their cross products are equal. |  | 84 |
| 3525020235 | Proportion | A proportion is an equation with a ratio (fraction) on each side. |  | 85 |
| 3524526205 | Similar Polygons | Polygons are similar when their corresponding angles are congruent and the ration of their corresponding sides are in proportion. |  | 86 |
| 3524553455 | Similarity Ratio | Ratio of corresponding sides |  | 87 |
| 3525149045 | Solving a Proportion | To solve a proportion, cross multiple and solve the equation for the unknown. |  | 88 |
| 3525285370 | Transformation of a figure | Transformation is a change in position, shape, or size of a figure. |  | 89 |
| 3351605723 | Coordinate Plane | A plane that is divided into four regions by a horizontal line called the x-axis and a vertical line called the y-axis. |  | 90 |
| 3525403940 | Isometry | Transformation of a figure in which the pre-image of a figure and the image of the figure are congruent. |  | 91 |
| 3525331488 | Translation of a Figure (sliding motion) | Translation is a transformation that moves points the same distance and in the same direction. - A Translation DOES NOT change the orientation of the figure. - A Translation is an isometry. Example: (x-7, y-3) algebraic notation or <-7,-3> vector notation |  | 92 |
| 3525346913 | Reflection of a Figure (The Flip) | - A Reflection changes the orientation of the figure - A Reflection is an isometry |  | 93 |
| 3525492553 | Rotation of a figure (Turn) | A rotation is a transformation where a figure is turned about a given point (center of rotation). A Rotation is an isometry. |  | 94 |
| 3525492554 | Dilation of a figure | A dilation is a transformation that produces an image that is the similar to the pre-image (original figure). A dilation stretches or shrinks the pre-image. The description of a dilation includes the scale factor (or ratio) and the center of the dilation. |  | 95 |
| 3525649486 | Center of Dilation | A point about which the figure is dilated. |  | 96 |
| 3525550021 | Scale Factor | The amount by which the image grows or shrinks is called the "Scale Factor". SF > 1 --> Image is enlarged (larger) 0 < SF < 1 --> Image is reduced (smaller) SF = 1 --> Image is the exact same size as the original (Isometry). |  | 97 |
| 3576140187 | Clockwise Rotation | Right Turn |  | 98 |
| 3576142788 | Counterclockwise Rotation | Left Turn |  | 99 |
| 3579896054 | Horizontal Line | A horizontal line is one the goes left-to-right, parallel to the x-axis of the coordinate plane. All points on the line will have the same y-coordinate. A horizontal line has a slope of zero. |  | 100 |
| 3579897841 | Vertical Line | A vertical line is a line that goes straight up and down, parallel to the y-axis of the coordinate plane. All points on the line will have the same x-coordinate. The slope of a vertical line is undefined. |  | 101 |
| 3579876743 | Equations of horizontal and vertical lines | Graph horizontal line: y=3, y=-4, etc Graph vertical libe: x=3, x=-7 etc |  | 102 |
| 3581900343 | Pre-image | The original figure |  | 103 |
| 3581901031 | Transformation Image | The transformed figure |  | 104 |
| 3599295515 | Circle - Arc | Part of the circumference of the circle |  | 105 |
| 3599299037 | Circle - Measure of Minor and Major Arcs | The measure of an arc is equal to the measure of the central angle. Measure of Minor Arc < 180 degrees Measure of Major Arc > 180 degrees |  | 106 |
| 3599298268 | Circle - Measure of Minor Arc | The measure of a minor arc equals the measure of its central angle. |  | 107 |
| 3599302416 | Circle - Measure of Major Arc | The measure of a major arc equals 360 minus the measure of the minor arc. |  | 108 |
| 3599299488 | Circle - Measure of a Semicircle | The measure of a a semicircle equals 180 degrees. |  | 109 |
| 3599297042 | Circle - Arc Length | Part of the circumference of the circle. |  | 110 |
| 3599327877 | Circle - Sector | A sector is a region bounded by two radii of a circle and the intercepted arc of the circle. |  | 111 |
| 3599297776 | Circle - Area of Sector | The number of square units it takes to exactly fill a sector of a circle. |  | 112 |
| 3599330961 | Circle - Chord | Chord: A line segment with the endpoint on the circumference of the circle. Diameter: A cord that passes through the center of the circle. |  | 113 |
| 3599343021 | Tangent | A line that "just touches" the circle at one point. |  | 114 |
| 3675869170 | Central Angle | An angle formed at the center of a circle by two radii. The vertex of a central angle is always the center of the circle. The measure of a central angle is equal the measure of the intercepted arc. |  | 115 |
| 3675835286 | Inscribed Angle | An angle is inscribed in a circle if the vertex of the angle is on the circle and the sides of the angle are chords of the circle |  | 116 |
| 3675848484 | Central Angle Theorem | The measure of the inscribed angle (∠ABC) is always half the measure of the central angle (∠AOC) when both angles intercept the same arc AC. |  | 117 |
| 3704508146 | Special Right Triangle 45-45-90 | Right Isosceles triangle. Both legs are equal. Hypotenuse= Leg * √ 2 |  | 118 |
| 3704541517 | Special Right Triangle 30-60-90 | Short Leg is opposite the smallest angle (30°). Long Leg is opposite the 60° angle. Long Leg = (short leg) *√3. Hypotenuse = 2 * Short Leg |  | 119 |
| 3704587380 | Square Roots and Perfect Squares Chart | A square root is a number that, when multiplied by itself, will result in a given number. |  | 120 |
| 3704627414 | Radical Expression | A radical expression is defined as any expression containing a radical (√) symbol. |  | 121 |
| 3704646707 | Multiplication and Division properties of Square Roots |  | 122 | |
| 3704682298 | Simplify Square Roots | To simplify a square root, you "take out" anything that is a "perfect square". |  | 123 |
| 3704658858 | Radical Expressions and how to Rationalize the Denominator | When you have a fraction with a radical in the denominator, you can use a technique called rationalizing a denominator to eliminate the radical. Multiply numerator and denominator by the radical that converts the denominator into a square root of a perfect square. |  | 124 |
